Reaktor 如何让两个数永远不相等

作者：曾照南

在数学里，要让两个数永远不相等是一件很简单的事，随便举个例子，就拿正整数来说，找个跟1永远不相等的数，那这个问题的答案实在是太多了，只要是大于1的都是。那么要是把这问题再换一下，同样是正整数范围，如果是两个随机的数，如何确保它们永远不相等呢？好的，今天我就要在Reaktor里好好讨论这个问题。

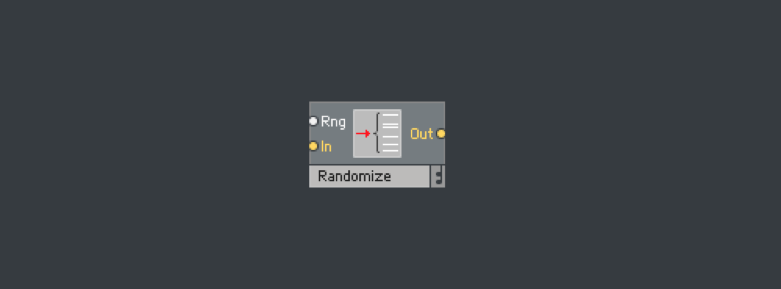
首先，要谈论随机的话，就需要一个能产生随机数的模块，Reaktor有为了用户提供了一个专门产生随机数的模块，它叫Randomize（尽管它不是真正的随机）。（图1.1）

图1.1

这个模块有两个输入，Rng输入是用来设定随机的范围，比如Rng设置为1，随机数可选范围是-1到1，但要注意的是，并不包含-1和1，而In则是一开始的数值，这个数值将会跟Rng随机选择后的数值相加并输出到Out；当然这里我不打算讨论实数，我想要让随机的结果是正整数，除此之外，我还需要有个随机数值范围，比如最大值为16，而最小值为1，然后让最终随机的范围落在1到16（包含最大值和最小值）。

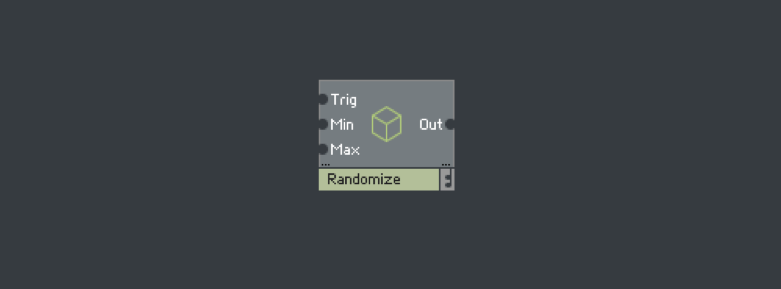
好的，有了上面的要求，我就开始搭建一个可以产生随机正整数的模块出来，通常一开始，我都喜欢创建一个Macro，并给它命名为Randomize，然后添加相应的输入和输出。（图1.2）

图1.2

可能很多人会奇怪为什么第一个输入要用Trig（Trigger意思就是触发），而不用In了，其实这是个人命名上的习惯问题，当然有些想说用In来命名也是可以的，只是要注意的是，我这里的Trig是有它特定的意思，因为它就是要用来告知是否有事件通过，它跟事件的数值没有任何关系。

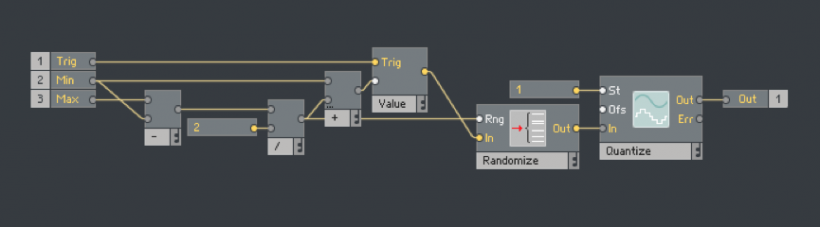
好的，接下来怎么让随机数落在我们设定的范围呢？方法很简单，我们可以用特殊化去到正常化，假设最大值16、最小值1，那么可以把最大值减去最小值，也就是16减去1，得到了15，然后再把15除以2，得到7.5，而这个数值就是Rng要用到的，除了这个之外，别忘记了最小值也要加上这个数值。（图1.3）

图1.3

从图1.3可以看出了我上面用Trig的原因，这样一来，Randomize模块的In输入就是一个不变的数值，即8.5，Rng则是7.5，即随机数在-7.5到7.5之间，所以它最终的结果将会在1到16之间；不过这仅仅只是完成了开始的一部分，最后还有一个部分没完成，因为需要的最终结果应该是正整数，而上面的结果不是正整数，而是带有小数点的数（哈哈，其实就是有理数），所以我还需要去它进行取整。

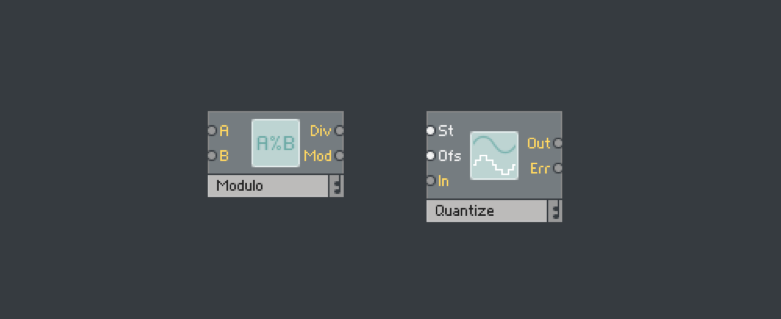
说到取整，Reaktor有提供了两个可以取整的模块，一个叫Modulo，另外一个叫Quantize（图1.4）。

图1.4

那么到底要用哪个呢？它们有什么区别呢？其实对于Modulo模块，它就像是一个floor运算，而Quantize模块则像是round运算，也就是说，无论数值小数点后面是多少，对于floor运算，它们通通都等于0，而对于round就不同了，只要是大于等于0.5的话，都等于1，否则等于0，但对于上面的随机取整很显然应该是要用Quantize模块，如果用Modulo模块，那么随机数永远到达不了最大值16，因为上面的随机数也有可能大于等于15.5（等于可能不好说，但大于肯定有），用Quantize再恰当不过了。（图1.5）

图1.5

到这里已经算是一个可以完成任务的模块了，不过我通常都会有个习惯，我会很在意模块的初始化状态，而实际上，图1.5会在Reaktor打开的时候产生一个随机数，具体原因就出在Value模块，所以为了避免触发Value模块从而去触发Randomize模块产生一个初始化的随机数，我可以添加一个Separator模块来避免这个问题，但同时也限制Trig的使用要求，也就是说Trig到达的事件数值必须大于0。（图1.6）

图1.6

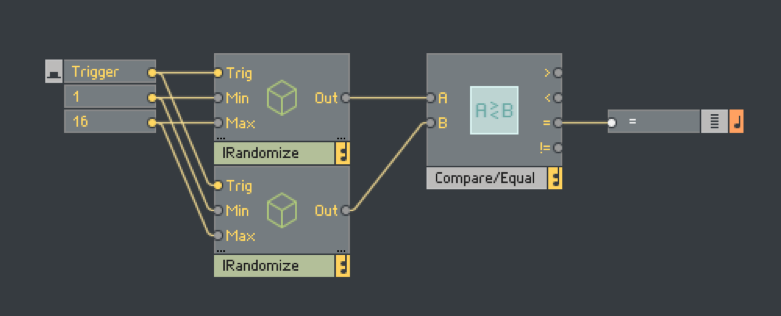
好的，我现在可以好好地使用这个刚搭建好的Randomize模块了，为了更好地区分原始模块Randomize模块，我决定在它前面加个大写的I，叫IRandomize（I这里的意思是integer的简称）；接下来，我需要去比较两个随机数是否相等，所以我需要再复制一个IRandomize，需要一个Compare/Equal模块。（图1.7）

图1.7

图1.7比较了两个随机数是否相等，如果相等的话，那么Compare/Equal模块的=输出就会输出1，否则0，但问题是除了比较，我要的结果是要让两个数永远不相等；OK，为了得到想要的结果，接下来可能开始有点复杂了。（图1.8）

图1.8

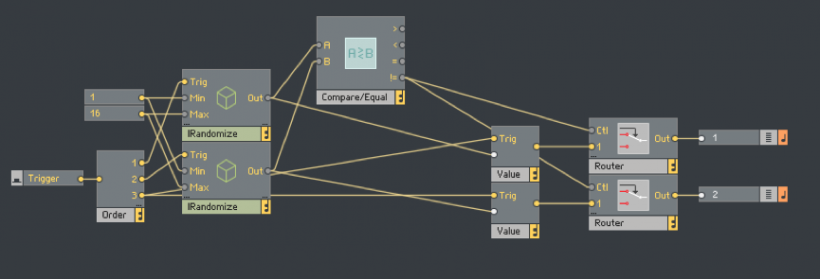
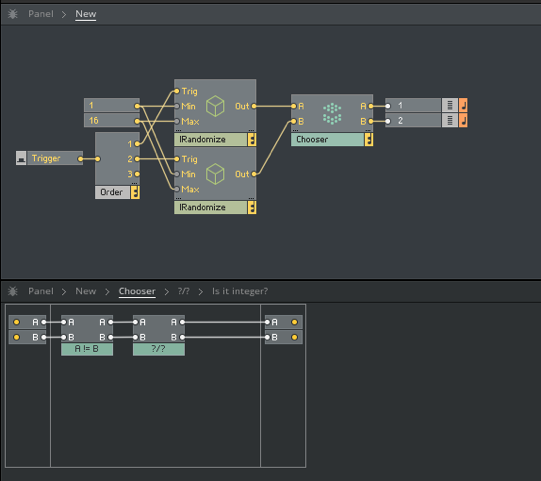
其实上面也不是很复杂，更多的是觉得连线开始有点乱了，但只要是逻辑清晰的话，都很容易看出来，为了能让大家看懂，我在这里就简单描述下：首先，我用到了Order模块，先去触发产生两个随机数进而判断是否不相等，然后通过Router模块去让它们不相等的结果通过，要注意，我还用到了两个Value模块去触发开始产生的随机数，原因是因为我想让Router先判断路由接口，再判断能否发送事件，所以这里必须要有Order模块的存在。

但是...但是到这里我并不想结束，我还想判断这两个随机数相除的结果是否是个整数，我的意思是指大的数除以小的数，所以我还需要对这两个随机数判断哪个是大的哪个是小的，当然方法有很多，我可以仍然用Compare/Equal模块和Router模块的组合，不过为了更好地去避免更多模块的连线（我指的是Primary Level的模块），我决定用Core Cell来是实现。

首先，我要创建一个Core Cell，给它命名为“A/B Or B/A”，然后添加相应的输入和输出。（图1.9）

图1.9

不过在搭建之前，让我先来理清一下逻辑，假设A大于B，那么A就除以B，相反，B就除以A；这个逻辑是没错，但有个问题是除数不能为0，这点非常重要，所以在一开始的时候，应该尽量避免随机数有产生0的可能性。好的，除此之外，如果两个数相等呢？这不就回到上面刚刚说过的问题了吗，因此我完全可以不需要上面Compare/Equal模块，直接把它也包含在Core Cell里去一次性完成，甚至也不需要Router模块和那两个Value模块。（这里应该知道Core Cell的魅力了吧）。

OK，我要先滤掉相等的情况，这可以通过创建一个Macro来实现（注意这里的Macro是Core Cell里的Macro），给它命名为“A!=B”。（图1.10）。

图1.10

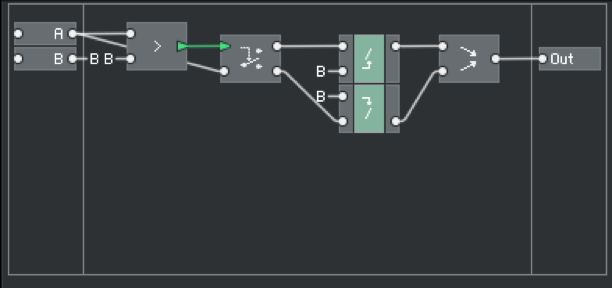
接下来，我要对这个Macro进行设计搭建，因为它的作用就是要滤掉相等的情况，所以同样的我也需要对它们进行判断，具体搭建结果如下图所示。（图1.11）

图1.11

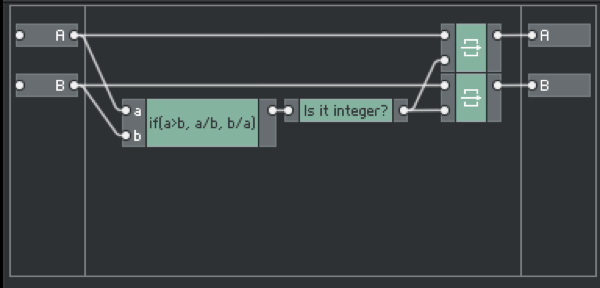
对于图1.11的搭建，相信很多人都能看得懂，唯独要注意的是A和B它们的先后顺序，这里用B作为Router的主要输入而不用A是因为A先产生随机数后B产生，如果用A作为Router的主要输入，那么结果可能会出现错误，最能测试这错误的就是判断它们是否不相等，如果相等，结果就输出1，反之输出0。（图1.12）

图1.12

而这种情况产生错误的原因是因为当A事件到达时，B还没有任何事件到达，所以在一开始跟A事件数值比较的是0，因此只要A事件数值不等于0，它都是会触发一个1的数值输出，

这样一来，B到达的事件数值就没有率先跟A事件数值比较，而当B事件数值到达后，尽管能跟A事件数值比较，但它没有连接到Router模块的输入，所以无法触发A和B比较的结果是否相等。

好的，知道“A!=B”为何要那样搭建，我就可以滤掉两个数相等的情况，但接下来重点的来了，我上面已经提到了，我还要判断这两个随机数相除的结果是否为整数，而在判断它们相除结果是否为整数之前，我又要先判断这两个随机数谁大谁小，因为我要的就是大的除以小的，所以我可以再创建一个Macro，给它命名为“？/？”，意思就是谁除以谁。（图1.13）

图1.13

要搭建这个功能的模块不难，我只要判断两个数谁大谁小，然后再来根据判断的结果选择谁除以谁，具体搭建结果如下图所示。（图1.14）

图1.14

注意，这里我用到了QuickBus的功能，因为我觉得如果B再使用连线的话，可能会造成这个搭建看起来很乱，而且可读性会大大降低。

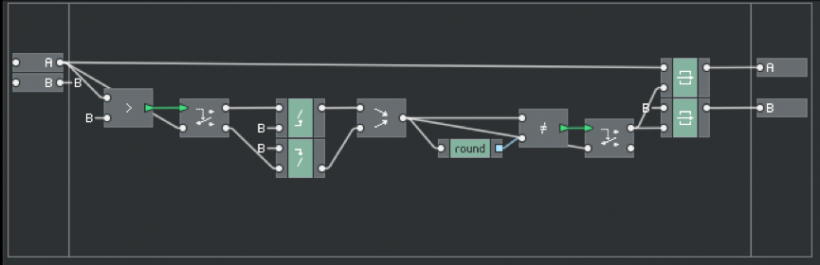
单单上面那样还是不够的，我还要继续判断它们结果是不是整数，因为上面相除的结果可能会出现小数的部分，比如举个例子，2跟3，根据上面得出的结果应该是1.5，显然它不是整数，接下来的问题是我应该怎么去判断相除的结果是不是整数啊，更何况即使结果是一个整数，Reaktor也不会告诉你说，它就是一个整数！？有一个非常技巧性的方法就是，我可以对相除的结果取整，然后再把取整的结果跟原始的结果比较，如果它们相等的话，就说明结果就是一个整数，就拿2跟3的例子，相除结果等于1.5，给它取整，假设取整的结果等于1，那么1.5不等于1，假设取整的结果等于2，那么1.5也不等于2，倘若是2跟4的话，那么相除结果将等于2，而2无论怎么取整，它永远都等于2，因此判断的结果将会是2永远等于2，所以这里我可以得到一个结论就是，判断相除结果是不是整数，跟你取整到这个数的上限整数或下限整数没关系，只要判断它们不相等，就可以知道结果是不是整数；好的，有了这样的分析，要搭建的部分就不难了。（图1.15）

图1.15